RMSE
평균 제곱근 오차(RMSE)는 예측한 값과 실제 환경에서 관찰되는 값의 차이를 다룰 때 흔히 사용하는 측도이다.
예측값과 실제값의 오차는 양수, 음수 모두 나올 수 있기 때문에, 각 오차의 제곱의 평균을 구한뒤 이를 제곱근으로 정의한 것이 RMSE이다.
간단한 예시를 보자.
예시 데이터
rating_example=[[4, 3.5], [5, 5], [0.5, 1], [3, 5]]
rating_example = pd.DataFrame(rating_example, columns=['Actual', 'Predict'])
<결과>

실제값(Actual), 예측값(Predict)를 갖고 있는 간단한 데이터를 만들었다.
RMSE 계산
import numpy as np
# 오차 계산: error = Actual - Predict
rating_example['error'] = rating_example['Actual'] - rating_example['Predict']
# 오차의 제곱 계산: squared error: +와 -가 캔슬되는 것을 막기 위해서
rating_example['squared error'] = rating_example['error'] ** 2
# 평균 오차 계산(mse)
mse = rating_example['squared error'].mean()
# 평균 제곱근 오차 계산(rmse): root mean squared error: rmse
rmse = np.sqrt(mse)
//Result
1.0606601717798212이처럼 수학 계산을 그대로 코딩하면 rmse를 계산할 수 있다.
RMSE with sklearn
앞서 rmse를 계산하는 과정을 알아봤는데,
scikit learn 라이브러리는 이러한 과정을 간단한 함수로 제공한다.
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(rating_example['Actual'], rating_example['Predict'])
rmse = np.sqrt(mse)
//Result
1.0606601717798212mean_squared_error 함수에 실제값, 예측값을 인자로 넣으면 mse를 쉽게 구할 수 있다.
계산된 mse에 제곱근만 적용시켜 rmse를 간단히 계산한다.
앞으로 scikit learn의 mean_squared_error를 사용해 학습데이터를 기반으로 평가 데이터에 대한 예측을 하는 실습을 해보겠다.
사용 데이터
MovieLens 영화 데이터 -> ml-latest-small.zip -> ratings.csv
https://grouplens.org/datasets/movielens/
import pandas as pd
ratings = pd.read_csv('[파일 경로]/ratings.csv')

사용자(userId)가 영화(movieId)에 매긴 평점(rating) 데이터
Train Test Split
실습의 목적은 평가 데이터(Test)의 사용자(user)들이 영화(movie)에 대해 어떻게 평점(rating)을 부여할 것인지 예측하는 것이다.
- 예측 데이터(predict)는 이미 존재하는 학습 데이터(train)를 기반으로 만들고,
- 평가 데이터(test)와 예측 데이터(predict) 간의 rmse를 통해 얼마나 잘 예측했는지 확인해볼 것이다.
먼저 전체 데이터를 학습 데이터(train)와 평가 데이터(test)를 분리한다.
from sklearn.model_selection import train_test_split
train, test = train_test_split(ratings, random_state=42, test_size=0.1)
print(train.shape)
print(test.shape)
//Result
(90767, 4)
(10086, 4)전체 데이터(ratings)를 적당한 비율(test_size)로 학습 데이터(train)와 평가 데이터(test)로 분리한다.
+) random_state를 부여하는 이유는 매번 같은 규칙으로 섞도록 하기 위함이다. 즉, 매번 split할 때마다 학습, 평가 데이터가 달라지는 것이 아닌 고정될 수 있도록 한다. state 값은 어떤 것을 사용해도 무방하다.
결과를 보면 학습 데이터는 90%, 평가 데이터는 10% 비율로 데이터가 split된 것을 볼 수 있다.
예측하기
이제 영화 평점을 예측해보자. 몇 가지 상황에 대해서 예측을 해보겠다.
모두 0.5점으로 예측하기
간단하다. 모든 사람이 영화에 대해서 0.5점을 부여할 것이라고 예측해보자.
말도 안된다 생각할 수 있지만 예측 결과 어떻게 될지 확인이라도 해보자.
# 모든 사람이 0.5점: 0.5 * 평가 데이터만큼의 리스트 생성
predictions = [0.5] * len(test)
#rmse 계산
mse = mean_squared_error(test['rating'], predictions)
rmse = np.sqrt(mse)
//Result
3.173911788635354모두가 0.5점을 줄 것이라 예측했기 때문에 단순히 평가 데이터(test)만큼의 0.5 리스트를 만들고 rmse를 계산해보았다.
계산 결과 3.17의 의미는
-> 모든 사람이 0.5점을 부여할 것이라 예측한다면, 실제 평점은 평균적으로 약 3.17의 오차가 생길 것이다.
평점의 범위가 [0, 5]인 것을 생각하면 매우 큰 오차라고 할 수 있다.
실제로 전체 평점의 분포를 살펴보면,
train['rating'].hist()<결과>

대체로 3, 4, 5점 구간의 평점 분포가 많은 것을 볼 수 있다.
그래서 모두가 0.5점을 부여할 것이라 예측했을 때, 매우 큰 rmse가 계산된 것이다.
모두 5점으로 예측하기
그럼 반대로 모든 사람이 영화에 대해서 5점을 부여한다면 어떨까?
# 모든 사람이 5점: 5 * 평가 데이터만큼의 리스트 생성
predictions = [5] * len(test)
#rmse 계산
mse = mean_squared_error(test['rating'], predictions)
rmse = np.sqrt(mse)
//Result
1.8306769643844378rmse가 확연히 줄어들었다.
0.5점과 5점, 양 극단의 값으로 예측을 해보니 사람들은 대체로 평점으로 후하게 주는구나... 정도는 알 수 있겠다.
데이터의 평균으로 예측하기
이제 학습 데이터(train)을 사용해보자.
실제로 사람들이 평점을 매긴 학습 데이터의 평균값을 사용하면 더 정확하지 않을까?
# 학습 데이터의 평균
rating_avg = train['rating'].mean()
# 모든 사람이 평균: 평균 * 평가 데이터만큼의 리스트 생성
predictions = [rating_avg] * len(test)
#rmse 계산
mse = mean_squared_error(test['rating'], predictions)
rmse = np.sqrt(mse)
//Result
1.045071895924614실제 학습 데이터를 기반으로 예측하니 훨씬 정확해진 것을 볼 수 있다.
그렇다면 오차를 줄이기 위해서 학습 데이터를 통해 보다 정확하게 예측하는 방법은 없을까?
사용자 평점 기반 예측하기
단순히 학습 데이터 평점의 평균이 아닌, 각 사용자의 평균 평점으로 예측해보자.
ex)
userId 1번의 train 데이터 평균 평점이 4.33이라면, test 데이터에 있는 userId 1번의 모든 영화에 대한 평점을 4.33이라고 예측할 수 있다.
먼저 각 사용자(userId)에 대한 평점(rating)의 평균을 계산해보자. 평점의 평균은 예측 데이터이기 때문에 컬럼명을 predict로 하였다.
users = train.groupby('userId')['rating'].mean().reset_index()
users = users.rename(columns={'rating':'predict'})
<결과>
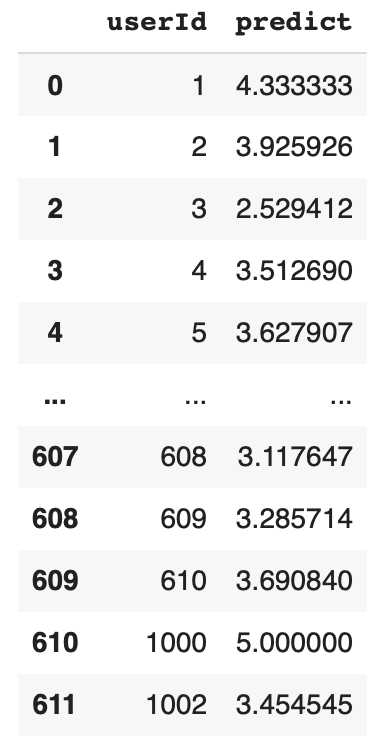
이제 평가 데이터(test)에 앞서 계산한 예측 데이터를 merge한다.
각 user 별로 실제 평점(rating)과 예측 평점(predict)를 확인할 수 있다.
predict_by_users = test.merge(users, how='left', on='userId')<결과>

그러나 예외 상황이 있을 수 있다.
만약 학습 데이터(train)에는 존재하는 userId가 평가 데이터(test)에는 없을 수 있지 않을까?
맞다. 평가 데이터라는 것은 학습 데이터와 별개로 새로운 user에 대해서도 예측할 수 있기 때문이다.
예측 데이터(predict) 역시 학습 데이터(train)을 기반으로 만들어진 것이기 때문에 평가 데이터(test)에 merge했을 때 값이 들어가지 않는 경우가 있을 것이다.
이러한 결측값이 얼마나 있는지 확인해보자.
predict_by_users.isnull().sum()<결과>
userId 0
movieId 0
rating 0
timestamp 0
predict 0
dtype: int64운이 좋았는지 결측값이 하나도 없다. 아마도 사용자 수가 적어서 그런지 split을 할 때 train, test 모두에 잘 들어갔나보다.
그럼 바로 rmse를 계산해보자.
mse = mean_squared_error(predict_by_users['rating'], predict_by_users['predict'])
rmse = np.sqrt(mse)
//Result
0.9406523982548508학습 데이터의 평균으로 예측했을 때보다도 오차가 더 줄었다...!
전체 평균보다 사용자별 평균으로 예측한 것이 더 정확하게 예측한 것이다.
왜 이러한 예측이 더 정확할까? 이번 예측은 다음 근거로 출발했었다.
예측의 근거)
- 영화에 대해 평균적으로 평점을 후하게 주는 사람은 다른 어떤 영화들이라도 후하게 줄거야.
- 반대로 박하게 죽는 사람들은 어떤 영화들이라도 박하게 줄거야. -> 그러므로 사용자 개개인 별로 예측해도 좋겠다!
실제 표준편차 계산을 통해 예측의 근거에 힘을 실어보자.
전체 학습 데이터의 표준편차를 계산해보자.
train['rating'].std()
//Result
1.0422913893252579-> 데이터가 전체 평균에서 1.04정도 떨어져 있다는 뜻이다.
이번엔 각 사용자별 평점의 표준편차를 계산해보자.
train.groupby('userId')['rating'].std().mean()
//Result
0.9247333128875478각 사용자 평점의 표준편차는 사용자가 평점을 얼마나 뒤죽박죽 주는지, 혹은 일정하게 주지에 대한 측도가 된다.
이에 대한 평균을 계산해보니 약 0.92로 전체 표준편차보다 작다.
이 값이 주는 의미는 각 사용자의 평점의 평균으로 분석했을 때가 전체 데이터의 평균으로 분석했을 때보다 오차가 적다는 것이다.
실제 그래프를 보자.
train.groupby('userId')['rating'].std().hist()<결과>
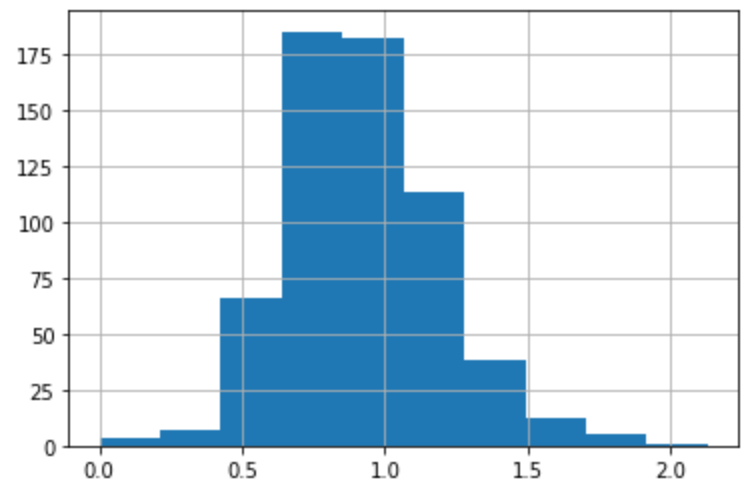
전체 평균인 1.04에 비해 각 사용자의 표준편차의 값들의 왼편으로 치우쳐져 있는 것을 볼 수 있다.
즉, 유저 표준편차가 전체 표준편차보다 예측의 질을 높일 수 있다.
다양한 상황에서의 rmse 분석을 통해 어떻게 데이터를 예측하는 것이 더 정확한지, 그에 대한 근거는 무엇인지 알아보았다.
데이터 예측은 이후 추천 알고리즘 등 다양한 ML 알고리즘에서 활용할 수 있으니 조금 더 공부해봐야겠다.
'python > data analysis' 카테고리의 다른 글
| [Google Colab] Github에 push 하기 (2) | 2022.05.19 |
|---|---|
| [Scikit learn] Linear Model을 사용한 컨텐츠 베이스 추천 + Lasso 모델 적용 (0) | 2021.09.06 |
| [Pandas] concat - 데이터 이어 붙이기 (0) | 2021.08.26 |
| [Pandas] 영화 평점 데이터 분석 (0) | 2021.08.26 |
| [Pandas] 멱함수 분포 (0) | 2021.08.26 |
![[Scikit learn] 학습데이터, 평가 데이터 평균제곱근 편차(RMSE) 계산](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FMfCtB%2FbtrdgRjBAa1%2Fy9p5wgJRZIxVLRl9nPO14k%2Fimg.png)